Binary Walsh Matricies/Codes will be uses the most of this conversation since the use of 1’s and 0’s allows for the use of boolean logic.
Start with 2×2 Binary Walsh Matrix…
W_2= \begin{bmatrix}0 & 0 \\0 & 1 \end{bmatrix}
The number of rows can be represented by a single bit, as can the number of columns. We can then generate a truth table for this matrix:
| R_0 | C_0 | f(R_0,C_0) |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
This shows that the function can be represented by the following expression:
f(R_0,C_0) = R_0 \bullet C_0
Stepping up to a 4×4 Binary Walsh Matrix…
W_4= \begin{bmatrix}0 & 0 & 0 & 0 \\0 & 1&0&1\\0&0&1&1\\0&1&1&0 \end{bmatrix} Here, the rows and columns can each be represented by two bits. So the first row is 00, the second row is 01, the third is 10, and the last row is 11. The same is done with the columns. Next, we can create a Karnaugh map by rearranging the rows and the columns as show below.
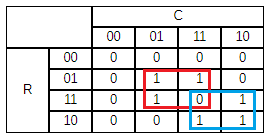
This allows us to create the following function to calculate the value at each position within the matrix:
f(R_0,R_1,C_0,C_1) = (R_0 \bullet C_0) \bullet \overline{(R_1 \bullet C_1)} + \overline{(R_0 \bullet C_0)} \bullet (R_1 \bullet C_1)An exclusive or is defined as:
A \oplus B = A\bullet \overline B + \overline A \bullet B
So the previous function can be simplified to be:
f(R_0,R_1,C_0,C_1) = (R_0 \bullet C_0) \oplus (R_1 \bullet C_1)
Stepping up one more time to a 8×8 Binary Walsh Matrix…
W_8= \begin{bmatrix}
0&0&0&0&& 0&0&0&0\\
0&1&0&1&& 0&1&0&1\\
0&0&1&1&& 0&0&1&1\\
0&1&1&0&& 0&1&1&0\\\\
0&0&0&0&& 1&1&1&1\\
0&1&0&1&& 1&0&1&0\\
0&0&1&1&& 1&1&0&0\\
0&1&1&0&& 1&0&0&1\\
\end{bmatrix} Three bits are now needed to represent the number of rows and columns.We can once again create a Karnaugh map by rearranging the rows and columns.
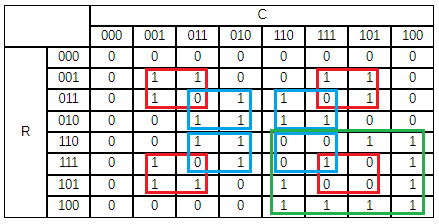
From this we can calculate the function for the values in the 8×8 matrix as follows:
f(R_0,R_1,C_0,C_1) = ((R_0 \bullet C_0) \bullet \overline{(R_1 \bullet C_1)} + \overline{(R_0 \bullet C_0)} \bullet (R_1 \bullet C_1))\bullet \overline{(R_2 \bullet C_2)} +
\overline{((R_0 \bullet C_0) \bullet \overline{(R_1 \bullet C_1)} + \overline{(R_0 \bullet C_0)} \bullet (R_1 \bullet C_1))}\bullet (R_2 \bullet C_2)To help simplify, let us define x, y, and z to be the following:
x = (R_0 \bullet C_0)\\ y = (R_1 \bullet C_1)\\ z = (R_2 \bullet C_2)
f(R_0,R_1,R_2,C_0,C_1,C_2) = (( x \bullet \overline y)+(\overline x \bullet y))\bullet \overline z + \overline{(( x \bullet \overline y)+(\overline x \bullet y))}\bullet z \\
= ((x\bullet \overline y \bullet \overline z) + (\overline x \bullet y \bullet\overline z)) + ((\overline x+y)\bullet(x+\overline y))\bullet z\\
= (x\bullet \overline y \bullet \overline z) + (\overline x \bullet y \bullet\overline z) + ((x\bullet\overline x) +(x\bullet y)+(\overline x\bullet\overline y)+(\overline y\bullet y))\bullet z\\
=(x\bullet \overline y \bullet \overline z) + (\overline x \bullet y \bullet\overline z) + (x\bullet y\bullet z) + (\overline x \bullet \overline y \bullet z) \\
= x \oplus y\oplus z
Replacing the values we substituted for x,y, and z…
f(R_0,R_1,R_2,C_0,C_1,C_2) = (R_0\bullet C_0)\oplus(R_1\bullet C_1)\oplus(R_2\bullet C_2)
Following the pattern, we can conclude that any 2^n by 2^n Walsh matrix can have the code character calculated as follows..
f(R_0,...,R_n,C_0,...,C_n) = (R_0\bullet C_0)\oplus ... \oplus(R_n\bullet C_n)
Typically the row defines the code word/sequence selected. So R is constant for a give code word/sequence. The column is incremented to step through each character of the code word/sequence. Discrete code generation logic could be designed to generate each code character. The row (R) selects the desired code word/sequence. Then the column (C) is incremented each time a character is encoded/decoded. Once C reaches 2^n, then it is reset to zero.