A 2x2x2 Hadamard Matrix can be constructed by inverting the two opposite corners of the matrix.
H_{2} = \begin{bmatrix} \begin{bmatrix}+1&+1 \\+1&-1 \end{bmatrix} \begin{bmatrix}-1&+1 \\+1&+1 \end{bmatrix} \end{bmatrix} This can be represented graphically by a 2x2x2 cube, where 1 is assigned the color white and -1 is assigned the color black.

It is clearly visible that the 2×2 Hadamard matrix is present in every face of the 2x2x2 matrix/cube.
Sylvester’s construction can be applied to create larger 3D Hadamard matrices in the same way it is applied to make larger 2D matrices.
H_{4} = \begin{bmatrix} \begin{bmatrix}1*\begin{bmatrix} \begin{bmatrix}1& 1 \\1&-1 \end{bmatrix} \begin{bmatrix}-1& 1 \\1&1 \end{bmatrix} \end{bmatrix} & 1*\begin{bmatrix} \begin{bmatrix}1& 1 \\1&-1 \end{bmatrix} \begin{bmatrix}-1& 1 \\1&1 \end{bmatrix} \end{bmatrix} \\1*\begin{bmatrix} \begin{bmatrix}1&1 \\1&-1 \end{bmatrix} \begin{bmatrix}-1& 1 \\1&1 \end{bmatrix} \end{bmatrix} &-1*\begin{bmatrix} \begin{bmatrix}1&1 \\1&-1 \end{bmatrix} \begin{bmatrix}-1& 1 \\1&1 \end{bmatrix} \end{bmatrix} \end{bmatrix} \begin{bmatrix}-1*\begin{bmatrix} \begin{bmatrix}1& 1 \\1&-1 \end{bmatrix} \begin{bmatrix}-1&1 \\1&1 \end{bmatrix} \end{bmatrix} &1*\begin{bmatrix} \begin{bmatrix}1&1 \\1&-1 \end{bmatrix} \begin{bmatrix}-1&1 \\1&1 \end{bmatrix} \end{bmatrix} \\1*\begin{bmatrix} \begin{bmatrix}1&1 \\1&-1 \end{bmatrix} \begin{bmatrix}-1&1 \\1&1 \end{bmatrix} \end{bmatrix} &1*\begin{bmatrix} \begin{bmatrix}1&1 \\1&-1 \end{bmatrix} \begin{bmatrix}-1&1 \\1&1 \end{bmatrix} \end{bmatrix} \end{bmatrix} \end{bmatrix} This comes out to be…
H_{4} = \begin{bmatrix} \begin{bmatrix}
1&1&1&1 \\
1&-1&1&-1\\
1&1&-1&-1\\
1&-1&-1&1 \end{bmatrix} \begin{bmatrix}
-1&1&-1&1 \\
1&1&1&1\\
-1&1&1&-1\\
1&1&-1&-1
\end{bmatrix} \begin{bmatrix}
-1&-1&1&1\\
-1&1&1&-1\\
1&1&1&1\\
1&-1&1&-1 \end{bmatrix} \begin{bmatrix}
1&-1&-1&1\\
-1&-1&1&1\\
-1&1&-1&1\\
1&1&1&1 \end{bmatrix} \end{bmatrix}Again, this can be represented, graphically as follows…
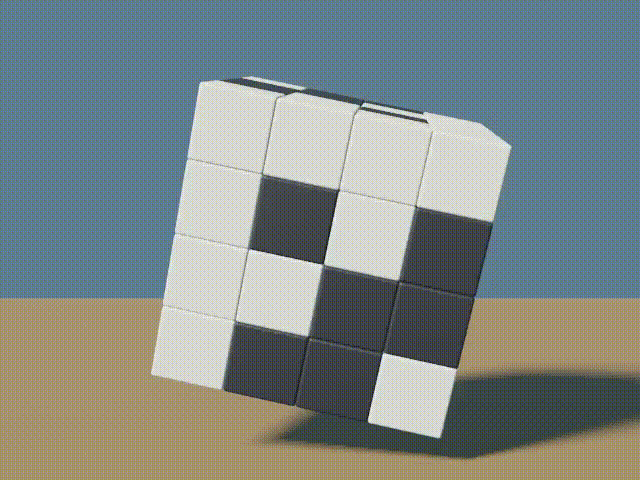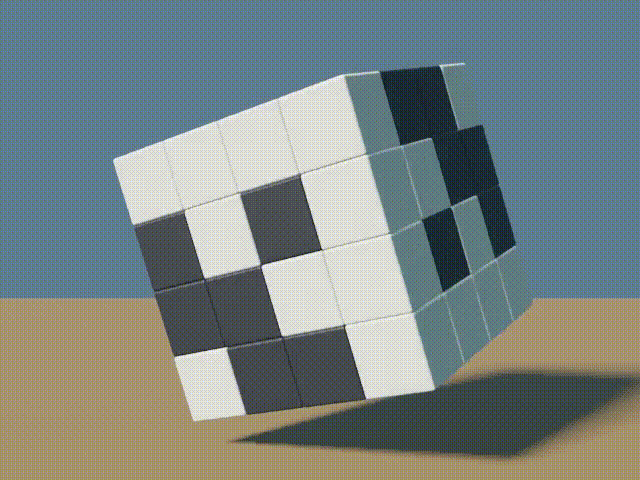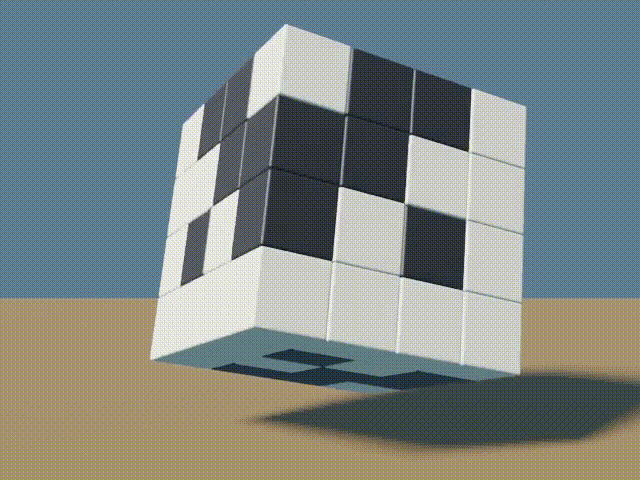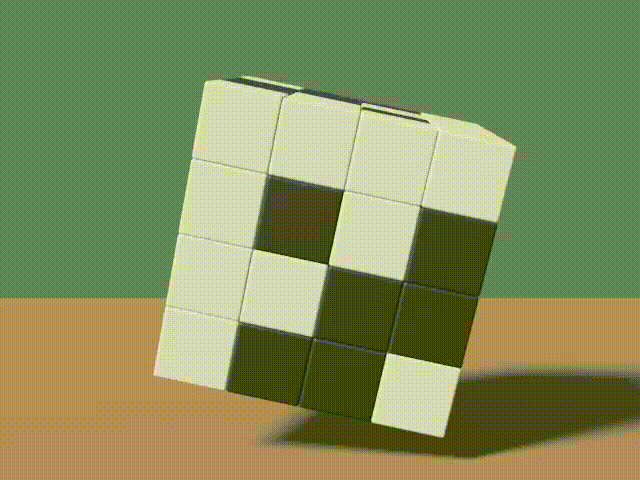
The next four images slice into the cube to show the 4 faces along the z-axis. Due to symmetry, the same could be done along any other axis.




All exterior faces are 4×4 Hadamard matrices. The interior faces are not 4×4 Hadamard matrices, however they contain the same proportion of positive and negative (or white and black) values as other faces, every row/column is different from every other row/column by exactly half the length.
Looking at the front face, if we label the rows A, B, C, and D. Where:
A = \begin{bmatrix}1&1&1&1 \end{bmatrix} \\
B = \begin{bmatrix}1&-1&1&-1\end{bmatrix} \\
C = \begin{bmatrix}1&1&-1&-1\end{bmatrix} \\
D = \begin{bmatrix}1&-1&-1&1 \end{bmatrix}The 4x4x4 cube can be represented as:
H_{4} = \begin{bmatrix} \begin{bmatrix}A\\B\\C\\D\\ \end{bmatrix} \begin{bmatrix}\overline{B}\\A\\ \overline{D}\\C\\ \end{bmatrix}
\begin{bmatrix}\overline{C}\\ \overline{D}\\A\\B\\ \end{bmatrix}
\begin{bmatrix}D\\ \overline{C}\\ \overline{B}\\A\\ \end{bmatrix} \end{bmatrix} Where the bar represents a negated/inverted pattern.
This shows that patterns A and C drop one row when moving from the first face to the last and patterns B and D raise one row.
If we assign the value of 1 to each non-negated pattern and -1 to each negated pattern, the previous matrix result in:
H_{4} (negated \enspace patterns)= \begin{bmatrix} 1&1&-1&1 \\1&1&-1&-1\\1&-1&1&-1\\1&1&1&1 \end{bmatrix} This is a upsidedown 4×4 Hadamard matrix.
Also, if create a 4×4 matrix, where the y-axis represents the pattern row 0=A, row 1=B, row 2=C, and row 3=D). and the x-axis represents each face of the cube. Then assign a value of +1 if the pattern was not inverted on that face and -1 if it was inverted,we get the following:
Negations = \begin{bmatrix}1&1&1&1 \\1&-1&1&-1 \\1&1&-1&-1 \\1&-1&-1&1 \end{bmatrix}This is also a 4×4 Hadamard matrix.
Sylvester’s construction can be used to create even larger Hadamard cubes.
The number of inversions (-1s) per row is always 1/2 the row length (with one row on every face having no inversions).
The number of inversions (-1s) per face and the number of inversions per cube can both be represented by the following formula, where n is the cube size (height, width, or depth):
Inversions = \frac{n-1}{2n}The limit as n approaches infinity is 1/2. Also exactly half of the entries in each row are different from the entries in every other row on that face. Furthermore, exactly half of the entries in each face are different from the entries in every other face of the cube. In other words, every row of a face is orthogonal from every other row and every face is orthogonal from every other face.
3D Hadamard Code Variant
An alternate variation of the 3D Hadamard matrix can be created by inverting one entry on the front face of a 2x2x2 matrix and then inverting all entries except the opposing corner on the back face.
H_{2}^{alt} = \begin{bmatrix} \begin{bmatrix}1&1 \\1&-1 \end{bmatrix} \begin{bmatrix}1&-1 \\-1&-1 \end{bmatrix} \end{bmatrix} This is represented by the following cube…

It is clearly visible that the 2×2 Hadamard matrix or an inverted matrix is present in every face of the 2x2x2 matrix/cube.
Once again Sylvester’s construction can be applied to create larger 3D Hadamard matrices…
H_{4}^{alt} = \begin{bmatrix} \begin{bmatrix}1*\begin{bmatrix} \begin{bmatrix}1&1 \\1&-1 \end{bmatrix} \begin{bmatrix}1& -1 \\-1&-1 \end{bmatrix} \end{bmatrix}&
1*\begin{bmatrix} \begin{bmatrix}1&1 \\1&-1 \end{bmatrix} \begin{bmatrix}1& -1 \\-1&-1 \end{bmatrix} \end{bmatrix} \\
1*\begin{bmatrix} \begin{bmatrix}1&1 \\1&-1 \end{bmatrix} \begin{bmatrix}1& -1 \\-1&-1 \end{bmatrix} \end{bmatrix}&-1*\begin{bmatrix} \begin{bmatrix}1&1 \\1&-1 \end{bmatrix} \begin{bmatrix}1& -1 \\-1&-1 \end{bmatrix} \end{bmatrix} \end{bmatrix} \begin{bmatrix}1*\begin{bmatrix} \begin{bmatrix}1&1 \\1&-1 \end{bmatrix} \begin{bmatrix}1& -1 \\-1&-1 \end{bmatrix} \end{bmatrix}& -1*\begin{bmatrix} \begin{bmatrix}1&1 \\1&-1 \end{bmatrix} \begin{bmatrix}1& -1 \\-1&-1 \end{bmatrix} \end{bmatrix} \\-1*\begin{bmatrix} \begin{bmatrix}1&1 \\1&-1 \end{bmatrix} \begin{bmatrix}1& -1 \\-1&-1 \end{bmatrix} \end{bmatrix}&-1*\begin{bmatrix} \begin{bmatrix}1&1 \\1&-1 \end{bmatrix} \begin{bmatrix}1& -1 \\-1&-1 \end{bmatrix} \end{bmatrix} \end{bmatrix} \end{bmatrix}This comes out to be…
H_{4}^{alt} = \begin{bmatrix} \begin{bmatrix}
1&1&1&1\\
1&-1&1&-1\\
1&1&-1&-1\\
1&-1&-1&1 \end{bmatrix} \begin{bmatrix}
1&-1&1&-1\\
-1&-1&-1&-1\\
1&-1&-1&1\\
-1&-1&1&1 \end{bmatrix} \begin{bmatrix}
1&1&-1&-1\\
1&-1&-1&1\\
-1&-1&-1&-1\\
-1&1&-1&1 \end{bmatrix} \begin{bmatrix}
1&-1&-1&1\\
-1&-1&1&1\\
-1&1&-1&1\\
1&1&1&1 \end{bmatrix} \end{bmatrix}And once gain, this can be represented, graphically as follows…
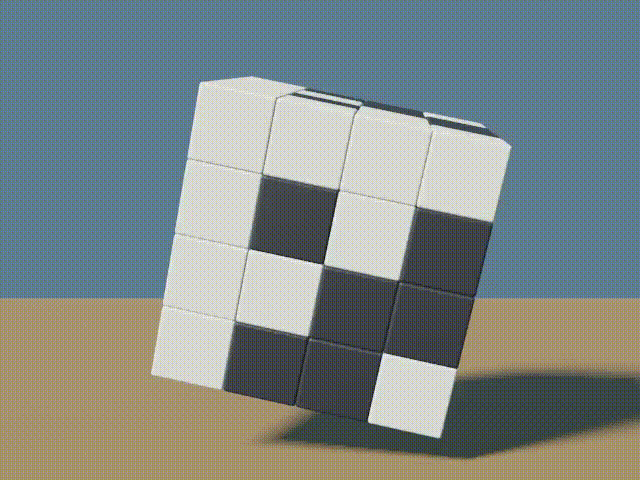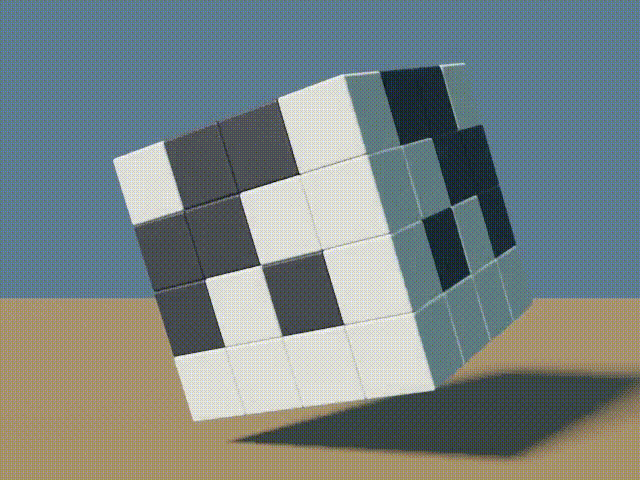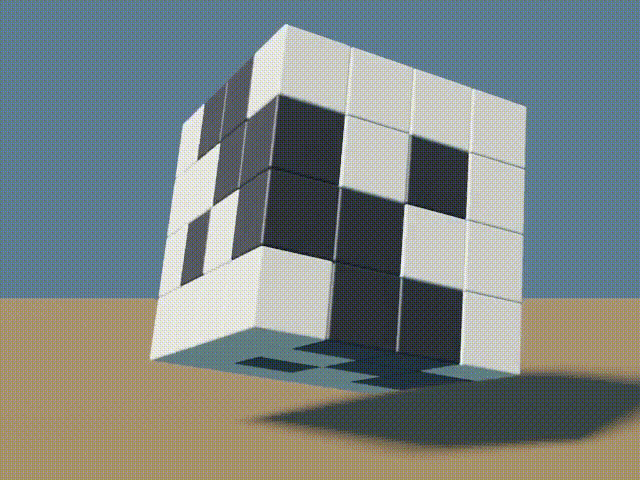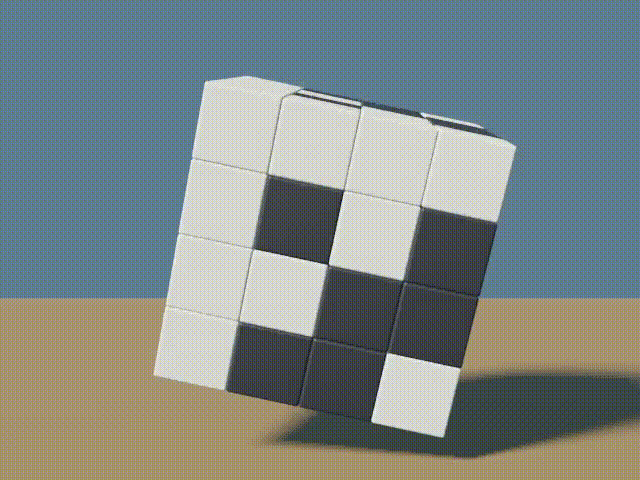
Again, Sysveter’s construction could continue to be used to create even larger cubes.
The number of inversions (-1s) per row is 1/2 the row length (with one row on every face having no inversions or every entry in the row inverted).
The number of inversions (-1s) per face can be represented by the following formula, where n is the cube size (height, width, or depth):
Inversions = \frac{n^2\pm n}{2n^2}The number of inversions per face still approaches 1/2 as n approaches infinity, however 1/2 the faces will have slightly under 1/2 of the entries inverted and 1/2 the faces will have slightly over 1/2 the entries inverted. This is because 1/2 the faces will have an entire row of non-inverted entries and the other 1/2 of the faces will have an entire row of inverted entries.
The number inverted entries in the cube is always 1/2 the total number of entries. It does not approach 1/2 as n approaches infinity. This is because 1/2 of the faces have an entire row that is not inverted and 1/2 the faces have an entire row that is inverted. These cancel each other out allowing the total number of inverted entries to equal 1/2 the total number of entries in the cube regardless of the cubes dimensions.
Once again, exactly half of the entries in each row are different from the entries in every other row on that face. Also, exactly half of the entries in each face are different from the entries in every other face of the cube. In other words, every row of a face is orthogonal from every other row and every face is orthogonal from every other face.